AlphaProof Paper

Thu 13 November 2025

I'm very excited to finally be able to share more details about how AlphaProof works! AlphaProof is the system that we used to discover the Lean proofs for the International Mathematical Olympiad 2024, reaching silver medal performance. Our full paper Olympiad-Level Formal Mathematical Reasoning with Reinforcement Learning has now been published in Nature. ^[1]

The International Mathematical Olympiad

The International Mathematical Olympiad, or IMO for short, is a yearly contest in mathematics amongst the 6 best high-school students from each of more than 100 countries all over the world. Problems include algebra, combinatorics, number theory and geometry, and are extremely challenging - usually less than 1% of participants achieve full marks on all problems.

The contest is divided into two days, with 4.5 hours each day to solve 3 problems. The maximum score per problem is 7 points, for a total of 42 points. Problem difficulty varies by year, so the cutoffs for gold, silver and bronze medals are actually set based on how many problems students manage to solve that year. In 2024, problems 3 and 6 were very difficult, with basically nobody being able to solve them:

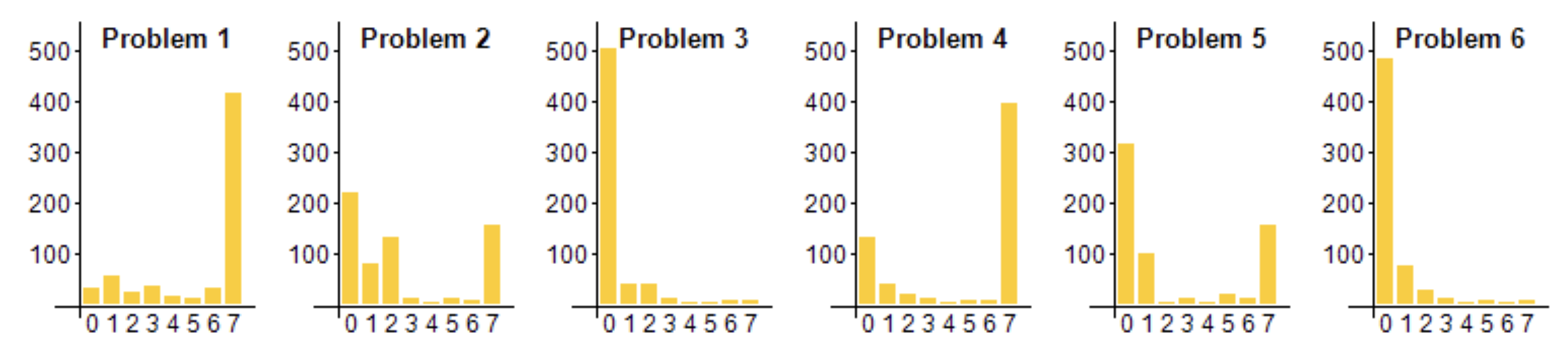
This resulted in a gold cutoff of 29 points, i.e. having to solve four problems completely and achieving partial marks on at least one problem. It's also possible to have easier problems, for instance in 2025 many students managed to solve 5 problems, resulting in a cutoff of 35 points.^[2]

The IMO problems for past contests are available online on the official IMO website; the Art of Problem Solving website also has community sourced solutions.

As an example, here's the easiest problem from 2024, problem 1:

Determine all real numbers $\alpha$ such that, for every positive integer $n$, the integer

$$\lfloor \alpha \rfloor +\lfloor 2\alpha \rfloor +\cdots +\lfloor n\alpha \rfloor$$

is a multiple of $n$.

Note that $\lfloor z\rfloor$ denotes the greatest integer less than or equal to $z$. For example, $\lfloor -\pi \rfloor =-4$ and $\lfloor 2\rfloor =\lfloor 2.9\rfloor =2$ .

Lean Programming Language

Lean is a formal language and proof assistant that can be used to write verifiably correct proofs that are still concise and human readable:

-- Every number larger than 1 has a prime factor
theorem exists_prime_factor :
    ∀ n, 1 < n → ∃ k, IsPrime k ∧ k ∣ n := by
  intro n h1
  -- Either `n` is prime...
  by_cases hprime : IsPrime n
  · grind [Nat.dvd_refl]
  -- ... or it has a non-trivial divisor with a prime factor
  · obtain ⟨k, _⟩ : ∃ k, 1 < k ∧ k < n ∧ k ∣ n := by
      simp_all [IsPrime]
    obtain ⟨p, _, _⟩ := exists_prime_factor k (by grind)
    grind [Nat.dvd_trans]

Lean is ideal for programmatic proof discovery:

• the syntax has similarities to both informal mathematics and programming languages, enabling generalization of pretrained LLMs
• a proof is composed of many short "tactics", providing a natural action space to search over
• partial proofs provide a concise "Lean state", describing the current assumptions and remaining goals to prove, which can be used to predict the next tactic
• verification of a proof given a theorem statement is entirely automatic, making it ideal for RL reward computation

Language Model

The first step in building our system was to design and train a suitable model that could predict good next tactics given the current Lean state. We had just wrapped up our work on AlphaCode, so naturally we turned to LLMs again. While Lean states can be very long (thousands of tokens), the individual tactics are usually very short (tens of tokens), so an encoder-decoder architecture seemed like the obvious first choice. This made it easy to embed the large Lean state once, then sample many tactics in parallel that all cross-attend to the same encoded state - allowing us to fit very large batch sizes and achieving high MFU.

Given the relatively small size of our transformer we chose to pretrain on a mix of only code and mathematical data, without using general natural language web data. To maximize the signal we could extract from this data we used a mixture of next token prediction and span reconstruction tasks, as well as dropout for regularization. This allowed us to benefit from training for 50 (!) epochs, resulting in 3 trillion tokens reconstructed by the decoder, and 12 trillion tokens seen by the encoder - scaling to many more epochs than observed in previous work.^[3]

Following pretraining we then fine-tuned the network on a small tactic dataset extracted from Lean mathlib, to ensure it was able to generate plausible Lean proofs from the start.

Tree Search

It was clear to us that Lean was perfectly suited to AlphaZero-style tree search:

• a proof consists of tens to hundreds of tactics, presenting a natural high-level action space
• the Lean interpreter makes for a natural environment, providing us with a new observation (the Lean proof state) after each tactic application
• the space of possible tactics is very large, and the choice of each tactic in a sequence has a big impact on all subsequent tactics

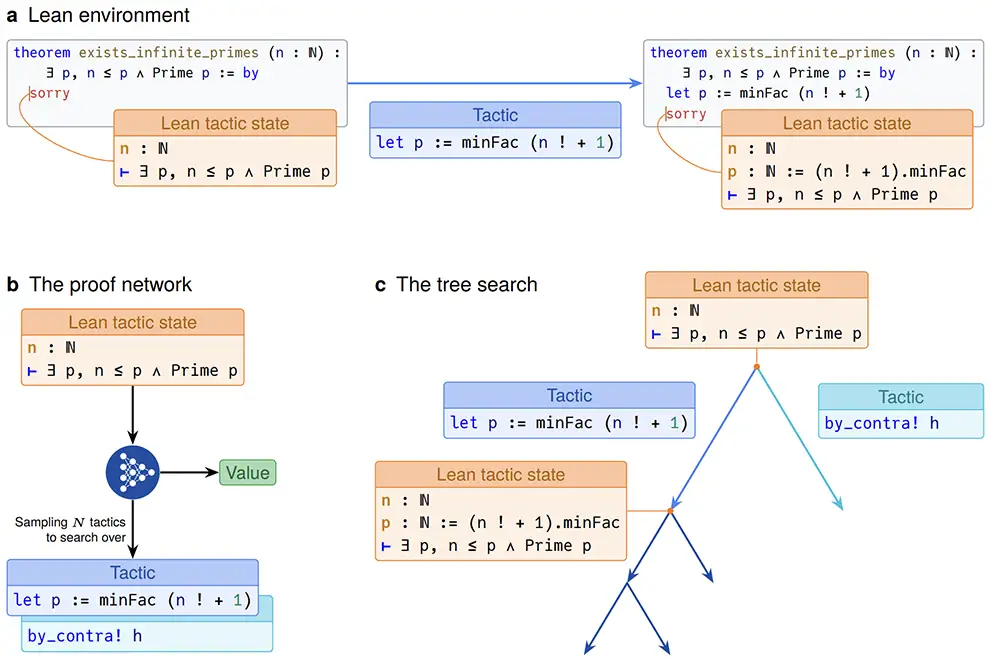
Lean has one additional property that we took advantage of: many tactics split a single goal into multiple sub-goals, each of which can be proved independently. A familiar example is induction: to prove that a statement holds for all $N$, we only need to prove a) that it holds for a base case $N=0$, and b) that if it holds for $N=k$ it also holds for $N=k+1$.

Rather than proving these sub-goals sequentially, we instead introduce a new type of node into our search tree: a product node (or and node), in contrast to the standard or node. Where in a standard or node we only need to prove one child to prove the node, for a product node we need to prove all children.^[4]

We originally referred to it as a product node because the probability of finding a proof for a product node is the product of the probabilities of finding proofs for all its child nodes. In contrast in a normal or node the probability would be the visit-count weighted average of the child node probabilities. ^[5]

This also informs how we back-propagate values through a product node: whereas in normal nodes we simply walk back up the tree and add in any intermediate reward observed along the way, every time we pass a product node we back-propagate the value of the hardest branch ^[6]. The intuition here is that the difficulty of finding a proof is directly based on how hard it is to prove its most difficult sub-statement.

This technique makes the search substantially more efficient:

• once we've found a proof for one child of a product node we can mark that child as proven and never need to visit it again
• we can adjust our action-selection and back-propagation formulas to choose whether to first focus on easy or on hard sub-proofs

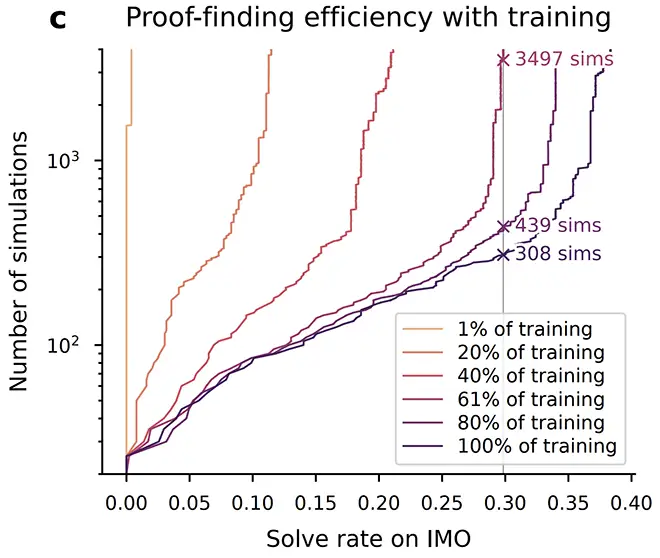
The resulting search scales well over many orders of magnitude of compute:

Reinforcement Learning

Now that we have a great RL environment and scalable search we are almost ready to run RL training, except for one complication: We need a large set of theorems that we can try to prove!

Mathlib is growing quickly, but even so it only contains around 200k theorems, many of them auxiliary. And we've already finetuned on it to teach our model how to write Lean! Fortunately we can find many theorems in natural language, so we trained a second network to formalize theorem statements from natural language into Lean, and then used the resulting Lean statements in RL:

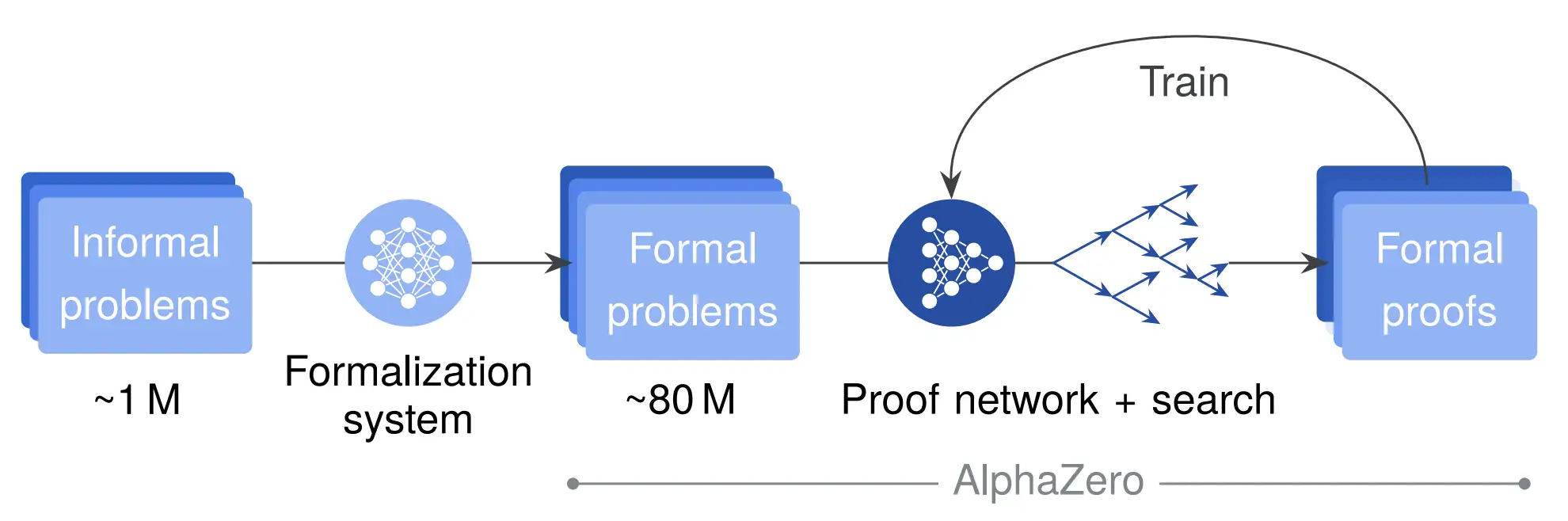
We obtain many more formalized statements (80) than original natural language statements (1M) because the formalization process is stochastic, both due to the nature of sampling from an LLM and because we intentionally randomized our prompts to obtain more distinct formalizations. There are often many different ways to formalize a statement, and some formalization attempts may be "incorrect" ^[7], in that they don't match the semantics of the natural language statement. The beauty of a formal language like Lean is that such an "incorrectly" formalized statement can still give us useful RL training data, as it is still a valid mathematical statement, and any proof we discover is guaranteed to be a valid mathematical proof.

The resulting large set of formal statements allowed us to run a lot of RL training, with consistent performance improvements on both train and test sets:

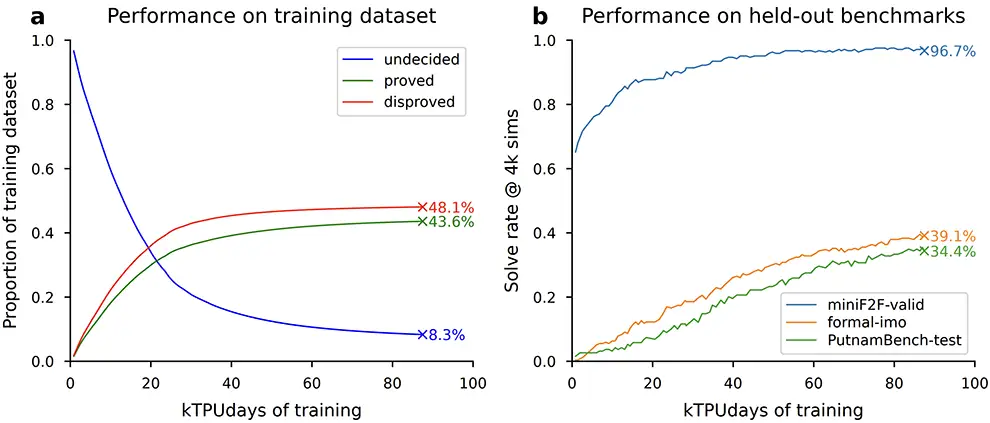
To maximize efficiency of training, we built a component to carefully track the progress on each formalization - once we disprove an invalid formalization there is no point in trying to prove it anymore. On the other hand, once we found a successful proof we do attempt the same problem again, as it is quite likely that AlphaProof will now be able to discover an even better, shorter proof.

Similarly we also want to manage the amount of search used: at the beginning of training we start with small searches to avoid wasting compute on problems that are still too hard, and to quickly find all easy proofs and disproofs. We then incrementally ramp up the amount of search over successive attempts on the same problem.

Test-Time RL

At the end of large-scale RL training we obtain a powerful proof network, which we can directly use to find proofs for novel theorems. However, for important problems that are worth the investment, we have another technique that allows us to invest more compute to obtain better results: test-time RL.

The procedure is very similar to our normal RL training, except this time instead of formalizing many different natural language statements we use an LLM to create many different variations of the theorem that we are interested in proving:

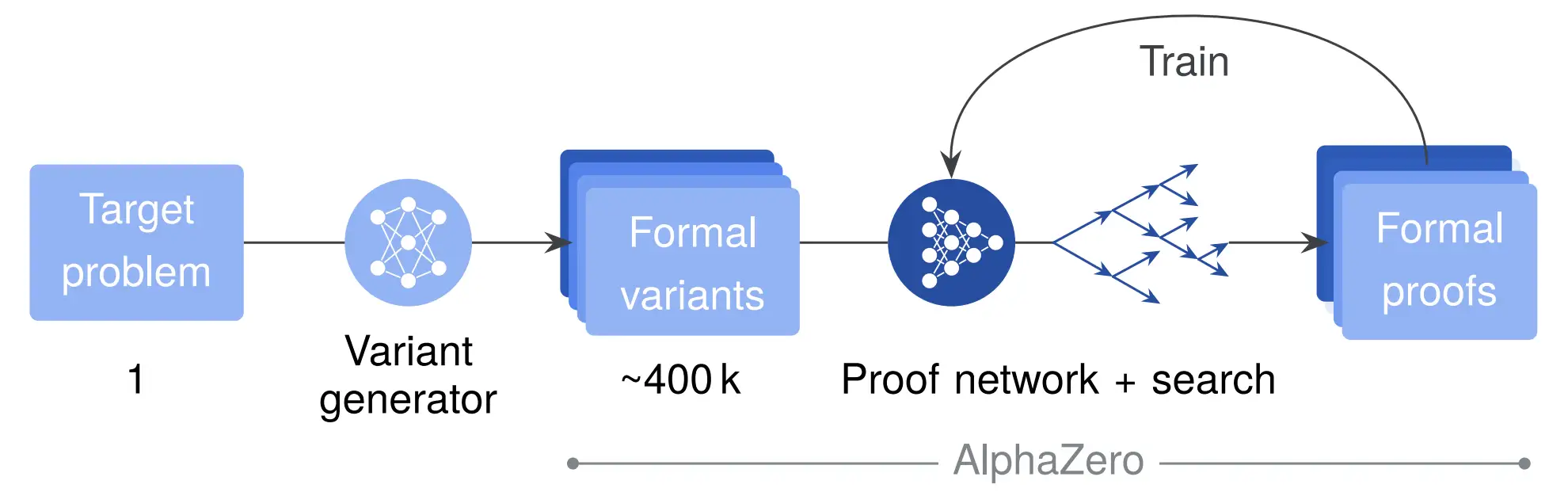
This process provides a natural curriculum, where some variants are likely to focus on easier sub-parts of the problem, and others may provide related, similar theorems.

IMO Proofs

Test-time RL is the algorithm that we actually ran for IMO 2024, resulting in proofs for IMO problems P1, P2 and P6.

I was especially excited that AlphaProof managed to discover a proof for P6, the hardest of all the problems for the human participants. Only 5 of the 609 participants managed to get the full 7 points on problem 6!

For very helpful explanations of the most important ideas in AlphaProof's Lean proofs I recommend this post by my friend Rishi: AlphaProof's Greatest Hits

What's Exciting

Aside from just being a really fun project to work on, I'm excited about AlphaProof for a few more reasons:

1. In contrast to current common language models that operate purely in natural language, AlphaProof produces outputs in formal language that can be verified automatically. No need to trust the model or manually check the output, no hallucinations to worry about, even for the hardest problems!
2. AlphaProof demonstrates the scalability of test-time compute to obtain improved answers over many orders of magnitude. The limit here was entirely how many TPUs we could get our hands on!
3. It's just the beginning! We still have many ideas for how we can make AlphaProof better as well as more general, now that we have shown that the principles of RL with search work just as well for LLMs.

For more details, please read the full paper, including the methods section! And if anything is unclear I'm happy to answer questions in the comments below.

1. The work described was done from the beginning of 2022 to July 2024, while I was still at Google DeepMind. ↩

2. See the Math Olympiad Hardness Scale for an exhaustive discussion of IMO problem difficulty. ↩

3. Note that the loss by no means plateaued, with more patience (and compute) we could have pretrained for many more epochs. ↩

4. For the product node naming, also see the Curry–Howard correspondence of logical conjunction (and) and product types. ↩

5. Note that while we initially experimented with directly using the probability of finding a proof as our value target, we actually settled on using the number of tactics left until the end of the proof. This is because probability of proving suffers from two major problems: a) it is almost always possible to revert a Lean tactic with a subsequent tactic, so the probability is only well defined if we assume some time or compute budget for the search. b) if we only train on valid proofs (which is useful from a quality filtering perspective) then all our training targets would be 1!. ↩

6. It's also possible to back-propagate the product of the branch values, but we found that using the value of the hardest branch performed better. ↩

7. Amusingly, if our search managed to find a proof for such a formalized statement too easily, that was usually a good sign that the formalization was wrong. ↩

Tags: ai, math, lean, llm, rl, mcts